Le test de khi-deux avec R
Nous allons maintenant réaliser le test de khi deux avec R car sa réalisation est fort simple et rapide. Cette facilité d'usage permet de passer plus de temps sur ce qui est le plus important : l'interprétation et l'analyse des résultats.
Méthode : Mise en œuvre
1) Importer les données
2) Créer un tableau de contingence (comme on l'a vu au chapitre précédent)
3) Appliquer sur le tableau de contingence la fonction chisq.test()
4) Analyser les résultats du test
Remarque :
Avec R pour connaître les arguments, les options et la signification d'une fonction, il suffit d'utiliser la commande help() ou ? :
help(chisq.test)
ou bien
?chisq.test
Ces commandes ("help()" et "?") permettent d'ouvrir l'aide de R. Elles fonctionnent avec toutes les commandes de R (avec Ubuntu pour quitter l'aide appuyez sur la touche "q").
Téléchargeons le fichier "variables.csv" dans lequel figure les réponses aux questions :
"Durant la semaine qui s'est écoulée combien de fois avez-vous utilisé l'informatique pour faire la classe ? une fois ou moins / plus d'une fois"
"Quelle discipline enseignez-vous ? histoire géographie/langues/lettres/math/autres".
Dans cet échantillon, constitué par les réponses de 173 enseignants de collège en France en 2009, y a-t-il un lien statistique entre la fréquence d'utilisation de l'informatique en classe et la discipline enseignée ? Réalisons un test de khi-deux pour le savoir.
Importation des données
D'abord, plaçons le fichier "variables.csv" dans le répertoire de travail de R[1]
Ensuite, importons les données qui sont contenus dans le fichier "variables.csv" :
read.csv2("variables.csv" , sep=";" , header=TRUE , na.strings="NA")->bdd
Remarquez que par rapport au chapitre précédent nous avons ajouté l'élément na.strings="NA" dans la commande read.csv2(). Lors de la réalisation d'une enquête par questionnaire il y a toujours des non-réponses, des données manquantes. Cette absence de réponses aux questions peut être codée de différentes façon. Dans le fichier "variables.csv" les non-réponses sont codés par "NA" qui signifie "Non Available" c'est à dire "non disponible". L'élément na.strings="NA" indique que les données manquantes sont codés par "NA". Si les non-réponses avaient étaient codé par rien, si les cases du tableau qui leurs correspondent avaient été laissées vides, on aurait indiqué na.strings=""
Création du tableau de contingence
2) Créons maintenant un tableau de contingence comme on l'a vu au chapitre précédent :
Examinons ce tableau ( que l'on appellera
) pour voir si les conditions d'application du test sont réunis : est-ce que chaque case du tableau à un effectif supérieur ou égal à 5 et est-ce que les effectifs totaux du tableau sont supérieurs à 60 ?
Oui, c'est le cas, le test de khi deux de contingence a du sens pour tester le lien statistique entre les lignes et les colonnes du tableau nous pouvons continuer.
Nous posons donc l'hypothèse d'indépendance : il n'y a pas de différence significative entre ces deux variables. Voyons si cette hypothèse est acceptable ou non.
Plaçons notre tableau de contingence dans un objet que nous appelons tableau :
table(bdd[,1] , bdd[,2])->tableau
Exécution du test de khi deux de contingence
Appliquons la commande chisq.test() sur notre tableau
chisq.test(tableau)
R répond alors :
Pearson's Chi-squared test
data: tableau
X-squared = 22.1801, df = 4, p-value = 0.0001845
Plaçons les résultats du test dans un objet :
chisq.test(tableau)->khideux
Examen des résultats et premières conclusions
Examinons le résultat du test :
> khideux
Pearson's Chi-squared test
data: tableau
X-squared = 22.1801, df = 4, p-value = 0.0001845
R indique d'abord qu'il applique le test de khi deux de Karl Pearson qui est son "inventeur" :
Pearson's Chi-squared test
Ensuite le test est appliqué sur l'objet "tableau" :
data: tableau
La valeur de l'indicateur de khideux est 22,18 :
X-squared = 22.1801
Le nombre de degrés de liberté est 4 :
df = 4
La probabilité d'avoir un indicateur de khi-deux de 22,18 pour 4 degrés de liberté est de moins de 0,001 (1 pour mille) :
p-value = 0.0001845
En général on accepte l'hypothèse d'indépendance lorsque p-value est supérieure à 5 % (0,05).
En l'occurrence p-value est inférieure à 1 pour mille (0,001) on rejette donc largement l'hypothèse d'indépendance. On peut donc affirme avec moins d'une chance sur mille de se tromper qu'il existe un lien statistique entre les lignes et les colonnes de notre tableau
.
Interprétation des résultats et conclusions finales
Analysons maintenant les effectifs des modalités qui s'éloignent le plus de l'indépendance.
La commande khideux$observed permet d'afficher notre tableau d'origine (
)
La commande khideux$expected permet d'afficher le tableau d'indépendance ou tableau des effectifs théoriques (
)
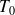La commande khideux$residuals permet d'afficher le tableau des résidus (
ou bien
)
Dans la section précédente, à partir du tableau
, on a calculé les tableaux
,
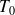et enfin
.
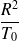Présentement, R a réalisé ces calculs à notre place mais ne présente pas le tableau des écarts à l'indépendance (
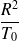) mais le tableau
appelé tableau des résidus (residuals).
Le tableau des résidus
présente l'intérêt d'indiquer le "sens" des écarts grâce au signe (positif ou négatif) qui figure dans chaque case du tableau. Tandis que le tableau des écarts à l'indépendance
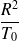permet de calculer l'indicateur de khi-deux. Pour calculer le tableau des écarts à l'indépendance il suffit de multiplier le tableau des résidus par lui même : khideux$residuals*khideux$residuals ou de l'élever au carré : khideux$residuals^2
On voit grâce au tableau des résidus ou au tableau des écarts à l'indépendance que ce sont les disciplines "autres" et "math" qui sont les principales responsables du calcul de l'indicateur de khi-deux.
En effet, les enseignants des disciplines "autres" sont significativement plus nombreux que les autres enseignants à déclarer utiliser l'ordinateur plus d'une fois par semaine. Inversement les enseignants de math sont significativement plus nombreux que les autres à déclarer utiliser l'ordinateur en classe moins d'une fois par semaine.
Remarque :
En résumé voici les commandes pour effectuer un test de khi deux de contingence avec R :
read.csv2("variables.csv" , sep=";" , header=TRUE , na.strings="NA")->bdd
chisq.test(table(bdd[,1] , bdd[,2]))->khideuxkhideux$observedkhideux$expectedkhideux$residuals
