Variance et écart-type avec R
Tout d'abord il faut saisir les données et les placer dans un objet que nous appelons « xi » :
c(3.88, 4.09, 3.92 , 3.97, 4.02, 3.95, 4.03, 3.92, 3.98, 4.06)->xi
Fondamental :
Dans R le séparateur décimal est le point « . ». On rentrera donc toujours les données décimales avec un « . » en guise de « , ». Peut être avez vous remarquez que la virgule est réservée a une autre fonction comme lorsque je saisis la distribution : 10,5 11 12 ainsi xi<-c(10.5, 11, 12)
Remarque :
Dans R la touche "flèche vers le haut" affiche la commande que l'on vient de saisir et permet de ne pas ressaisir la totalité d'une commande lorsque l'on a fait une erreur.
On peut maintenant effectuer le calcul de la variance par étapes :
Calcul de la moyenne de la distribution : mean(xi)->moyenne ou bien sum(xi)/10->moyenne
Calcul des
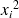 :
: xi^2->xicarres
Calcul de la moyenne des carrés : mean(xicarres)->moydescarres
Calcul de la variance : moydescarres-moyenne^2->variance
Calcul de l'écart-type grâce à la fonction racine carrée "sqrt()" : sqrt(variance)->ecartype
ecartype
[1] 0.06384356
On pouvait aussi le faire en une seule ligne :
la variance : mean(xi^2)-mean(xi)^2
l'écart type : sqrt(mean(xi^2)-mean(xi)^2)
De la même façon que pour Calc le calcul automatique réalisé par R nous donne les valeurs sans biais :
var(xi)
sd(xi)
Remarque : var signifie variance et sd signifie "standard deviation"







