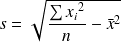Variance et écart type
L'écart type mesure la dispersion d'une distribution autour de la moyenne. En quelque sorte, l'écart type évalue la « largeur moyenne » de la distribution, il s'exprime donc dans la même unité que la variable.
Plus l'écart-type est faible, plus la distribution est homogène. Autrement dit, plus l'écart type est petit, plus les valeurs de la distribution sont proches les unes des autres. À l'inverse, plus l'écart type est grand, plus la distribution est étalée : plus les valeurs sont éloignées les unes des autres.
La variance
Pour calculer l'écart-type d'une distribution il faut auparavant calculer la variance. En effet, l'écart-type est la racine carré de la variance. La variance est noté
tant dis que l'écart-type est noté
.
Pour calculer la variance il existe un moyen mnémotechnique : « la variance est la moyenne des carrés moins le carré de la moyenne ».
Voyons ce que cela veut dire.
La moyenne des carrés
Que signifie "la moyenne des carrés" ?
Les carrés sont les valeurs de la variable
élevées au carré (multiplié par eux-mêmes), donc
noté
.
Pour trouver la moyenne des carrés il suffit d'appliquer la formule de la moyenne : la somme de la distribution des carrés, divisée pas le nombre de termes soit
divisé par
donc :
Voilà pour "la moyenne des carrés".
Le carré de la moyenne
Voyons maintenant ce que signifie "le carré de la moyenne"
C'est simplement la moyenne de la distribution multipliée par elle même :
soit
La moyenne des carrés moins le carré de la moyenne
Reprenons donc notre moyen mnémotechnique :
« la variance (
) est la moyenne des carrés (
) moins le carré de la moyenne
» la formule est donc :
Rappelez-vous on note la moyenne
(x barre) on peut donc aussi écrire la formule de la variance ainsi :
L'écart type
L'écart-type est la racine carrée de la variance que l'on va donc noter ainsi :
ou ainsi
Exemple :
Reprenons l'exemple de notre bucheron.
Calculons la variance de cette distribution :
Calculons maintenant l'écart-type :
L'écart type de cette distribution est d'à peu près 0,064 mètre soit 64 millimètres.
