Une première étape dans la constitution d'un ensemble d'indicateurs est de reprendre ceux qui ont été éprouvés dans l'espace et dans le temps par d'autres. S'il s'agit d'élaborer un questionnaire il peut être fructueux de le faire après avoir réalisé des entretiens puis des observations puis des entretiens sur les observations. Tout cela dans l'idée de rechercher à saisir la subjectivité des acteurs.
Il est donc nécéssaire de prendre soin d'élaborer ou de reprendre des indicateurs dont on expliquera leur pertinence. De la même façon il sera rigoureux de décrire comment on a constitué son échantillon et comment on a recueilli les données.
Pour analyser ces données statistiques je vous propose d'utiliser le logiciel R. Essentiellement parce que c'est un logiciel gratuit.
On trouvera des informations sur ce logiciel sur le site de framasoft.
Table des matières
- Table
des matières
- 1. Statistiques univariées
- 2.
Statistiques multivariées
- 2.1 Entrer des données
- 2.2 La régression linéaire : calcul de la droite d'ajustement d'un nuage de points par la méthode des moindres carrés
- 2.3 La regression linéaire avec R
- 2.3bis Analyse des séries chronologiques
- 2.4 Le test de khi deux
- 2.5 le khideux avec R
- 2.5bis Le V de Cramer
- 2.6 L'AFC
- 2.7 L' ACM
- 2.7bis l'ACP
- 2.8 AFC avec R
- 2.9 L'ACM avec R
- 2.10 La classification ascendante hiérarchique
- 3. Références bilbiographiques non-mises en forme
1. Statistiques univariées
1.1 Les différents types de variables
"Les individus d'une population sont observés sous l'angle d'un
caractère. Une variable statistique permet d'associer à
chaque individu de la population une modalité de ce
caractère" (J.L. Monino, J.M. Kosianski & F. Le cornu,
2004). Une variable est dite quantitative si elle est quantifiable (comme par exemple le nombre d'enfants illégitimes ou la quantité d'argent sur un compte en Andorre).
Une variable est dite qualitative si elle n'est pas quantifiable (comme par exemple le jugement porté sur la qualité d'un repas mangé au fouquètsse (bon, pas terrible, atroce) ou la couleur de 4x4).
Une variable quantitative est dite discrète si ses modalités prennent des valeurs dans les entiers naturels N (comme le nombre d'enfants illégitimes ou le nombre de robinets en or massif dans une maison). Si les valeurs d'une modalité appartiennent à l'ensemble des nombres réel R elle est dite continue (la quantité d'argent sur un compte en Andorre).
Une variable qualitative est dite ordinale si ses modalités possèdent une relation d'ordre (la qualité d'un repas au Fouquets : bon, pas top, à vomir).
Sinon elle est dite nominale (couleur de 4x4).
On peut transformer une variable quantitative en variable qualitative ordinale en effectuant des regroupements par classe.
1.2 Entrer des données dans R
R est un logiciel et un langage de programmation qui est "orienté objet". En pratique cela signifie que l'on peut attribuer à un objet (une lettre, un mot, une phrase) une ou plusieurs valeurs numériques, un ou plusieurs objet, des modalités, des fonctions ...Pour donner une valeur la valeur 12 à un objet n il suffit de taper :
n<-12 ou bien n=12
Pour qu'un objet n représente la distribution : 1, 8, 10, 7, 4, 3
n<-c(1, 8, 10, 7, 4, 3)
Pour entrer une distribution un terme à la fois :
n<-scan() puis entré les valeurs au clavier en tapant entré quand on a terminé.
Pour connaître la valeur d'un objet n il sufift de taper n. On peut aussi appeller un objet "maison" ou bien "kjhfgfksdjhgs".
Pour connaître les objets que l'on a crée on tape : ls ()
help("ls") permet d'avoir la liste des fonctions de ls. La fonction help s'applique à toutes les fonction pour avoir de l'aide.
On peut aussi taper
?ls
nb : Sous linux pour quitter l'aide taper : ":q" sans les guillemets
Dans un objet on peut mettre des objets :
name<-(n , n1<-2 , n2<-34883)
Pour effacer on utilise la fonction rm ()
rm () efface tout
rm (n) efface l'objet n
rm (n, n1) efface l'objet n et n1
1.3 Les différents types d'objets
[à faire]1.4 écarts types moyennes médiane etc. avec R
1.4.1 Variables quantitatives
Si d est une distribution constituée de valeures numériques positives ou nullesmean(d) fait la moyenne arithmétique de d
var(d) fait la variance de d
sqrt(var(d)) fait la racine carré de la variance donc l'écart type de d
sd(d) fait aussi l'écart type de d
sum(d) fait la somme des termes de d
summary(d) donne des élèments statistiques
fivenum(d) présente d'autres élèments statistiques
d^2 fait dxd termes à termes
length(d) compte le nombre de termes de d
d[2] affiche le 2ème terme de d
d[-2] affiche tout les termes de d sauf le 2ème
d[1:5] affiche les 5 premiers termes de d
d[d>3] affiche les termes de d supérieures à 3
max(d) et min(d) affiche les termes max et min de d
d[2]<-35 remplace le deuxième terme de d par 35
lenght(d[d>20]) affiche le nombre de termes supérieur à 20
1.4.2 Variables qualitatives
Imaginons que l'on interroge 5 personnes et que leur réponses respectivent soient : oui non non oui nonPour rentrer ces données dans R et les utiliser on peut le faire ainsi :
x<-c("oui" , "non" , "non" , "oui", "non")
table(x) fait un tableau récapitulatif
factor(x) présente les différentes modalités
barplot(table(x)) fait un diagramme baton
table(x)/length(x) présente la fréquence de chaques modalités
pie(table(x)) fait un camenbert
1.5
Les graphiques avec R
plot(1 , 1) fait un graphique de pointsLes options de la fonction plot sont, comme pour une grande partie des fonctions graphiques de R, les suivantes :
donne un nom aux axes sur le graphique
xlim=c(-2, 2) et ylim=c(-2 , 2) limite les axes à 2 et -2
main="titre" donne un titre au graphique
type="p" pour point
"l" pour line
"b" pour both
"h" pour un histogramme
1.6 Télécharger/installer/utiliser une librarie
Pour télécharger et installer une library faire :install.packages() puis choisir un mirroir et enfin la library
Pour charger une librairie avant d'utiliser les commandes qu'elle permet d'utiliser :
library("nom_de_la_librarie")
2. Statistiques multivariées
2.1 Entrer des données
*Pour créer la matrice :matrix(c(1, 2, 13, 14, 5, 6, 7, 8, 9, 10, 11, 12), 4, 3) où 4 et 3 sont respectivement le nombre de lignes et le nombres de colonnes.
*Pour créer un tableau de contingence :
Si vous avez un tableau de contingence dans excel, enregistrez le au format .txt avec tabulation comme séparateur puis confirmez deux fois. On obtient ainsi un fichier .txt lisible dans R.
Il faut mettre ce fichier dans le repertoire de travail. Pour connaître le repertoire de travail de R tapez : getwd().
Pour que cela marche bien il faut éviter les espaces (on peut les remplacer par des _ ), les signes de ponctuations et les caractères accentués.
Pour manipuler un tableau de contingence dans R on peut donc taper :
n<-read.table("nomdufichier.txt")
Il est aussi possible de lire des données en lignes. j'ai mis sur le site un fichier que vous pouvez lire en tapant par :
read.table("http://mehdikhaneboubi.free.fr/insee.txt")
*Si vous voulez modifier les données dans un tableur tapez
edit(n)
Pour sauvegarder il suffit de créer un nouvel objet :
m<-edit(n)
*Autre méthode pour créer un tableau de contingence :
Imaginons que l'on veuille créer un tableau de contingence à trois lignes et trois colonnes dont les noms des modalités des lignes sont : aaa, bbb, ccc et les noms des modalités des colonnes : ddd, fff, ggg .
-faire une matrice m
-créer deux objets nomlignes et nomcolonnes :
nomlignes<-c("aaa", "bbb", "ccc")
nomcolonnes<-c("ddd", "fff", "ggg")
-Puis intégrer les étiquettes dans la matrice ainsi :
rownames(m)<-nomlignes
colnames(m)<-nomcolonnes
et voilà m est un tableau de contingence.
*Si m est un tableau de contingence pour calculer les marges :
-des lignes : apply(m, 1, sum)
-des colonnes : apply(m, 2, sum)
2.2 La régression linéaire : calcul de la droite d'ajustement d'un nuage de
points par la méthode des moindres carrés
On cherche une droite de régression linéaire qui résumera le nuage de
 points
points
 de coordonnées
de coordonnées
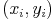 où
où
 .
.Pour ce faire on va remplir un tableau. Ce tableau va nous permettre d'aboutir à l'équation de la droite d'ajustement
 , au calcul du coefficient de régression linéaire
, au calcul du coefficient de régression linéaire
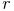 , au calcul de la variance résiduelle et de la variance expliquée.
, au calcul de la variance résiduelle et de la variance expliquée.Dans un tableur remplir les colonnes des
 et des
et des
 puis calculer
puis calculer
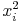 ,
,
 et
et
 ainsi
que leur sommes et leurs moments
ainsi
que leur sommes et leurs moments
 soit
la somme de chaque colonne divisée par
soit
la somme de chaque colonne divisée par
 .
.
La moyenne des
 est :
est :

La moyenne des
 est :
est :

La variance des
 est :
est :

La variance des
 est :
est :

Les écarts types
 et
et
 sont les racines carrés des variances.
sont les racines carrés des variances.La covariance des
 et des
et des
 est :
est :
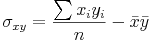
Si la droite de d'ajustement est
 alors la pente
alors la pente
 est égale à la covariance
est égale à la covariance
 des
des
 et des
et des
 sur la variance des
sur la variance des
 :
:
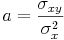
l'ordonnée à l'origine
 est égale à la moyenne des
est égale à la moyenne des
 moins la pente
moins la pente
 multipliée par la moyenne des
multipliée par la moyenne des
 :
:

Le coefficient de corrélation
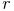 est la variance sur l'écart type des
est la variance sur l'écart type des
 multiplié par l'écart type des
multiplié par l'écart type des
 :
:

Pour calculer les valeurs des point projetés
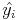 on effectue :
on effectue :
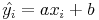
L'erreur est égale à :
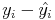
La variance résiduelle est égale à :

La variance expliquée est :

Pour vérifier que tout est juste on sait que la variance des
 est égale à la variance résiduelle plus la variance expliquée :
est égale à la variance résiduelle plus la variance expliquée :

2.3 La regression linéaire avec R
A titre d'exemple entrons la distribution et
et
 :
:> xi<-c(1:12)
> xi
[1] 1 2 3 4 5 6 7 8 9 10 11 12
> yi<-c(40, 42, 44, 45, 48, 50, 52, 55, 58, 63, 68, 70)
> yi
[1] 40 42 44 45 48 50 52 55 58 63 68 70
Pour obtenir l'équation de la droite d'ajustement écrire :
> lm(yi~xi)
Call:
lm(formula = yi ~ xi)
Coefficients:
(Intercept) x
35.076 2.745
ou bien faire :
> coef(lm(yi~xi))
(Intercept) x
35.075758 2.744755
où "Intercept" est l'ordonnée à l'origine
 et où "x" est la pente
et où "x" est la pente
 dans
dans

Pour obtenir le coefficient de corrélation linéaire
 :
:> cor(xi,yi)
[1] 0.9838759
Pour dessiner les points et la droite on fait :
plot(xi,yi,pch=3) ; abline(lm(yi~xi))
("pch=3" sert à faire que les points soit représentés par des croix plutôt que par des petits ronds) et on obtient le graphique ci-dessous

Pour obtenir les
 taper :
taper :> fitted(lm(yi~xi)
Pour avoir les
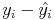 faire :
faire :> residuals(lm(y~x))
*Autre méthode pour avoir toutes les informations de la régression linéaire faire :
> summary(lm(yi~xi))
Call:
lm(formula = yi ~ xi)
Residuals:
Min 1Q Median 3Q Max
-2.2890 -1.6029 -0.1614 1.5728 2.7319
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 35.0758 1.1612 30.20 3.70e-11 ***
xi 2.7448 0.1578 17.40 8.35e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.887 on 10 degrees of freedom
Multiple R-Squared: 0.968, Adjusted R-squared: 0.9648
F-statistic: 302.6 on 1 and 10 DF, p-value: 8.355e-09
Où "Intercept" est l'ordonnée à l'origine, "xi" est la pente, "Multiple R-Squared" est le coefficient de régression linéaire au carré
*Si l'on veut un ensemble de graphiques avec des informations sur la régression linéaire on peut faire :
> plot(lm(yi~xi))
Si l'on veut que ces quatre graphiques apparaissent sur un seul document :
> par(mfrow=c(2,2)) ; plot(lm(yi~xi))

2.3bis Analyse des séries chronologiques
[à faire]
2.4 Le test de khi deux
La statistique du khi deux est une mesure des écarts entre des fréquences observées et des fréquences théoriques. Le test de khi deux permet de se prononcer, à un seuil de probabilité, sur la répartition des écarts entre les effectifs observés et les effectifs théoriques. Plus l’indicateur de khi deux est proche de zéro, plus les fréquences théoriques et les fréquences observées se confondent.
Le test de khi deux va permettre de répondre à la question « à partir de quelle valeur suffisamment grande des écarts doit-on dire que l’hypothèse d’indépendance n’est vraiment pas admissible » (Cibois, 1992). Le test du khi deux
On détermine à quel seuil de probabilité, on peut rejeter l’hypothèse nulle en consultant la table des fractiles de la loi de khi deux. G. MIALARET (Mialaret, 1991) indique qu’une des restrictions principales à l’utilisation de la technique de calcul du
D’un point de vue pratique, on calcule les totaux (les marges) de chaque ligne et de chaque colonne d’un tableau de contingence T
Puis on fait la différence terme à terme de T
En outre on calcule le pourcentage de contribution au khi deux pour chacune des cases du tableau pour pouvoir établir quelles sont les modalité responsable du calcul du khideux.
Comme le test de khi deux d'indépendance est sensible à la taille de l'effectif on peut éffectuer un V de Kramer qui s'il est proche de 0 indique une indépendance entre les lignes et les colonnes du tableau :
où
2.5 le khideux avec R
Avec la library par défaut :si n est un tableau de contingence :
chisq.test(n)
En guise d'exercice on peut faire un test de khideux de contingence "à la main"
Entrons notre tableau de contingence à trois lignes et trois colonnes dans une matrice t :
> t<-matrix(c(9, 14, 40, 9, 5, 8, 14, 11, 6),3,3)
> t
[,1] [,2] [,3]
[1,] 9 9 14
[2,] 14 5 11
[3,] 40 8 6
Calculons l'effectif total N :
> N<-sum(t)
> N
[1] 116
Calculons les marges :
> c(sum(t[,1]), sum(t[,2]), sum(t[,3]))
[1] 63 22 31
> c(sum(t[1,]), sum(t[2,]),sum(t[3,]))->margeslig
[1] 32 30 54
Vérifions que la sommes des marges lignes est égal à N :
> sum(margeslig)
[1] 116
Vérifions que la sommes des marges colonnes est égal à N :
> sum(margescol)
[1] 116
Faisons des matrices avec les marges et appelons les ml et mc :
> matrix(margeslig,3,1)->ml
> matrix(margescol,1,3)->mc
> ml
[,1]
[1,] 32
[2,] 30
[3,] 54
> mc
[,1] [,2] [,3]
[1,] 63 22 31
Calculons le tableau des effectifs théoriques :
> ml %*% mc
[,1] [,2] [,3]
[1,] 2016 704 992
[2,] 1890 660 930
[3,] 3402 1188 1674
> ml %*% mc->tt
> tt/N
[,1] [,2] [,3]
[1,] 17.37931 6.068966 8.551724
[2,] 16.29310 5.689655 8.017241
[3,] 29.32759 10.241379 14.431034
> tt/N->t0
Vérifions que la sommes des termes de t0 est égal à N :
> sum(t0)
[1] 116
Calculons le tableau de khi deux :
> (t-t0)
[,1] [,2] [,3]
[1,] -8.379310 2.9310345 5.448276
[2,] -2.293103 -0.6896552 2.982759
[3,] 10.672414 -2.2413793 -8.431034
> (t-t0)->r
> r*r
[,1] [,2] [,3]
[1,] 70.212842 8.5909631 29.683710
[2,] 5.258323 0.4756243 8.896849
[3,] 113.900416 5.0237812 71.082342
> r*r->rcar
> rcar/t0
[,1] [,2] [,3]
[1,] 4.0400246 1.41555643 3.471079
[2,] 0.3227331 0.08359457 1.109714
[3,] 3.8837297 0.49053756 4.925658
> rcar/t0->khideux
Calculons l'indicateur de khi deux :
> sum(khideux)
[1] 19.74263
Faisons faire le test de khi deux par R pour vérifier :
> chisq.test(t)
Pearson's Chi-squared test
data: t
X-squared = 19.7426, df = 4, p-value = 0.0005613
Pour finir calculons les tables des fréquences observées f et des fréquences théoriques f0 :
> t/N
[,1] [,2] [,3]
[1,] 0.0775862 0.07758621 0.12068966
[2,] 0.1206897 0.04310345 0.09482759
[3,] 0.3448276 0.06896552 0.05172414
> t/N->f
> t0/N
[,1] [,2] [,3]
[1,] 0.1498216 0.05231867 0.07372176
[2,] 0.1404578 0.04904875 0.06911415
[3,] 0.2528240 0.08828775 0.12440547
> t0/N->f0
[à faire calcul des contributions]
2.5bis Le V de Cramer
[à faire]
2.6 L'AFC
Selon P. CIBOIS (CIBOIS, 1992), l’Analyse Factorielle des Correspondances (AFC) est une méthode d’analyse des données qui permet de résumer l’information contenue dans un tableau de contingence T en le décomposant en une série de tableaux dont la somme terme à terme permet de le reconstituer. L’AFC va permettre de représenter en deux dimensions la majorité de l’information contenue dans un tableau T. On obtient la représentation graphique de la structure des écarts à l’indépendance qui est mesurée par le calcul de la contribution au khi deux. L’AFC va permettre de révéler les liens et les oppositions qui existent ou non entre les différentes modalités du tableau en fonction des écarts à l’indépendance.
La méthode se base sur le cadre théorique de l’algèbre linéaire, elle s’applique à un tableau de contingence d’au moins trois lignes et d’au moins trois colonnes, composé de valeurs entières, positives ou nulles. Elle est donc appropriée à l’analyse de tableaux croisés de deux variables qualitatives.
Cette méthode va calculer les coordonnées (les vecteurs propres) de chaque modalité des lignes et de chaque modalité des colonnes pour chaque dimension du tableau que l’on appelle les axes factoriels. On résume en général convenablement un tableau de contingence en extrayant de ce tableau cinq coordonnées par modalités.
Lorsque l’on effectuera un produit scalaire de ces vecteurs[1], on obtiendra un tableau qui sera un résumé du tableau initial mais par commodité, on utilise les vecteurs plutôt que les matrices, on peut ainsi représenter graphiquement ces vecteurs et obtenir une représentation graphique en deux dimensions de notre tableau T. Il s’agit donc de trouver des vecteurs qui résumeront notre tableau initial. G. SAPORTA[2] indique que P.CIBOIS a mis en évidence la propriété qui montre que l’analyse des correspondances étudie la structure des écarts à l’indépendance plus que les écarts eux-mêmes autrement dit l’AFC « met en relief la structure des écarts à l’indépendance, non leur intensité […]»[3].
Pour interpréter les résultats convenablement, il faut alors prendre en compte :
- les valeurs propres qui sont la quantité d’informations résumées par chaque axe. La somme totale des valeurs propres est égale à l’indicateur de khi deux du tableau initial et décrit la dispersion du nuage de points, les logiciels l’expriment généralement en pourcentage.
- les oppositions mises en évidence par les vecteurs propres entre les modalités des lignes et les modalités des colonnes sur chacun des axes.
- les contributions absolues qui permettent de connaître les modalités responsables de la construction d’un axe.
- les cosinus carrés (ou contributions relatives) qui indiquent la qualité de la représentation d’une modalité sur un axe. Plus le cosinus carré d’une modalité est proche de un, meilleure est la représentation de ce point.
L’AFC révèle la structure des écarts à l’indépendance ainsi que les attractions et les répulsions entre les modalités des lignes et les modalités des colonnes. Il faut mentionner que les points lignes et points colonnes (points profils) ne sont différenciés que par commodité d’usage et que l’AFC ne fait pas la différence entre les deux. Néanmoins, C. DERVIN[4] affirme que l’interprétation de la proximité entre les points lignes et les points colonnes est délicate et qu’il est prudent de bien prendre en compte les valeurs propres des axes et de toujours se reporter au tableau initial de données en cas de doute. En outre, L.LEBART, A. MORINEAU et M. PIRON[5] signalent que si le test de khi deux ne permet pas de rejeter l’hypothèse nulle, l’AFC pourra tout de même être utile pour décrire un nuage de points peu dilatés (qui ne permet pas de rejeter l’hypothèse nulle) mais dont la forme n’est pas sphérique (la répartition des points profils n’est pas due au hasard). Inversement, dans le cas d’un nuage de points très dilatés (on peut rejeter l’hypothèse nulle) mais avec une forme sphérique (la dispersion est uniforme), un test de khi deux permettra de rejeter l’hypothèse d’indépendance sans pour autant que l’AFC soit la meilleure méthode pour décrire la dépendance entre les lignes et les colonnes du tableau.
L’algorithme de l’analyse des correspondances qui permet d’extraire les vecteurs propres, les valeurs propres, les contributions absolues et les cosinus carrés d’un tableau de contingence est réalisé par tous les logiciels de statistiques. Néanmoins, G. SAPORTA[6] mentionne que « sur le plan mathématique, on peut considérer l’analyse des correspondances soit comme une analyse en composantes principales avec une métrique du khi deux soit comme une variante de l’analyse canonique ». On pourra consulter C.DERVIN[7], Y. DODGE[8], G. MIALARET[9] qui reprend P.CIBOIS[10] pour trouver des exemples d’AFC « pas à pas » et B.ESCOFIER et J. PAGES[11] ou J.M. BOUROCHE et G.SAPORTA[12] présentent une approche plus complète. Enfin, pour un exemple d’application de la méthode à la sociologie, on pourra se référer à W.DOISE, A. CLEMENCE et F. LORENZI-CIOLDI[13].
2.7
L' ACM
Si
l’AFC décompose
en facteur un tableau de
contingence composé de deux variables, l’Analyse des Correspondances
Multiples
(ACM) permet de
réaliser la même opération mais sur plus de deux variables, sur un
tableau dit
disjonctif complet. Dans ce cas, nous distinguerons deux types de
variables : les variables actives qui participent à la
construction des
facteurs et les variables supplémentaires qui n’y participent pas.
Comme une
modalité ayant peu d’observations sera plus éloignée de l’origine, il
est
conseillé, ou d’effectuer des regroupements entre les modalités, ou de
mettre
en variables supplémentaires les variables qui ont peu d’observations. L’interprétation est sensiblement la même que pour l’AFC. Néanmoins, B. ESCOFIER et J. PAGES indiquent que les valeurs propres et les pourcentages d’inertie ont peu d’influence sur l’interprétation d’une ACM ainsi que les cosinus carrés. « La qualité des représentations des modalités est elle-même un indicateur peu pertinent. En effet, les modalités d’une même variable étant orthogonales, elles ne peuvent être simultanément bien représentées sur un axe »[14]. On interprétera les résultats en s’appuyant sur les coordonnées des modalités, les contributions des modalités et sur la contribution d’une variable à un axe factoriel.
En pratique, C. DERVIN signale que pour bien réussir une ACM le nombre de modalités de chaque variable doit être voisin, les modalités doivent avoir des effectifs proches et qu’il faut éviter d’avoir des modalités trop rares. C.DERVIN propose comme règle empirique que l’effectif d’une modalité soit supérieur à racine carré de trois fois l'effectif total N.
En outre, il se peut que la projection des points profils sur les deux premiers axes ait une forme parabolique, c’est l’effet Guttman. B. ESCOFIER et J.PAGES précisent que « le fait d’identifier un effet Guttman ne modifie pas sensiblement l’interprétation des deux premiers axes d’une AFC (le premier axe est un facteur d’échelle, le second un facteur d’opposition entre les situations extrêmes et les situations moyennes). En revanche, cela conduit à négliger les facteurs suivants […]. »[15]
2.7bis l'ACP
[à faire]2.8 AFC avec R
2.8.1 Avec la library MASS
Aprés avoir chargé la library MASS en tapant :library("MASS")
créer un objet n avec un tableau de contingence à partir d'un fichier .txt comme présenté au point 1.4 puis taper :
m<-corresp(n , nf=2) nf est le nombre de facteur on peut l'augmenter
plot(m) et voila
2.8.2 Avec la library FactoMineR
>library("FactoMineR")Si t est un objet contenant un tableau de contingence comme par exemple la répartition des étudiants des universités de France en 2007 par discipline et par cursus selon le sexe d'après l'INSEE :
> t
lic_gar lic_fil mast_gar mast_fil doct_gar doct_fil
drt_sc_po 37317 69373 21693 42371 4342 4029
sc_eco_aes 49545 56961 29813 33649 2552 1983
lettre_lingui_arts 17850 48691 5853 17672 2401 4531
langues 21291 62736 3874 13186 907 1839
shs 41050 94346 20447 43016 6972 7787
sc_fond 54861 22559 48293 17078 11491 4407
sc_nat 15004 24318 8457 11090 5232 5641
staps 17253 8248 4172 1963 328 188
pluri_sc 11760 9009 785 602 108 37
med_odon 19005 36454 42797 59711 560 468
pharma 4010 7742 6244 13316 237 322
>afct<-CA(t) représente le premier plan factoriel
>afct donne les résultats d'un test de khi deux d'indépendance et indique les informations disponible à propos de l'afc qui vient d'être effectuée, par exemple
>afct$eig donne la variance et la variance cumulée pour chaque axes
>barplot(afct$eig[,2]) en donne la représentation graphique
>barplot(afct$eig[,2], names=paste("Axe", 1:nrow(afct$eig)), main="Inertie par axes") fait la même chose avec une légende
>plot(afct, axes=c(2,3)) représente le plan factoriel constirué par le 2ème et 3ème facteur
>plot(afct, axes=c(1,3)) représente le plan factoriel constirué par le 1er et 3ème facteur
>afct$col donne les coordonées des modalités des colonnes, leur contributions et leur cos²
>afct$row donne la même chose pour les lignes
>plot(afct) représente l'afc sur les deux premier axes
>plot(afct, invisible=c("col")) permet de n'afficher que les modalités des lignes
>plot(afct, invisible=c("row")) n'affiche que les modalités des colonnes
On obtient les graphiques suivant :


Les sciences dures (sc_fond) s'opposent sur le premier axe aux modalités caractérisant les filles qui sont en licence et en doctorat (lic_filles et doct_filles), tant dis que les shs, les lettres et les langues s'opposent aux modalités caractérisant les garçons qui sont en master et en doctorat (gar_mast et gar_doct). Sur le deuxième axe les garçons en doctorat s'opposent aux sciences de la vie et de la santé tant dis que les filles qui sont en master s'opposent aux staps.
2.8.3
Avec la library ade4
library("ade4")Si v est un tableau de contingence
dudi.coa(v)->d
scatter(d) fait le graphique
scatter.dudi(d) fait le graphique avec les vecteurs
inertia.dudi(d, col=TRUE, row=FALSE) : donne les contributions absolues des colonnes appelées col.abs et la contribution relative (les cos²) appelées col.rel
inertia.dudi(d, col=FALSE, row=TRUE)
Après avoir installer la librairie on obtient le graphique suivant avec le code suivant :
library("ade4")
read.table("http://mehdikhaneboubi.free.fr/insee.txt")->t
dudi.coa(t, nf=2)->afcinsee
2
scatter(afcinsee, posieig="none")

2.9 L'ACM avec R
[à faire]2.10 La classification ascendante hiérarchique
Nous allons voir maintenant comment réaliser une Classification
Ascendante Hiérarchique (CAH).Il s'agit de représenter un arbre
hiérarchique dans lequel sont classifier des modalités. On dit
classifier plutôt que classer car classer consiste à mettre dans des
classe tant dis que classifier consiste à ranger en fonction de ce que
l'on a ranger. Cet outil est donc utile pour établir des typologies et
pour bien interpréter les AFC, ACM et ACP.Nous allons regrouper les modalités les plus proches les unes des autres puis les groupes de modalités et ainsi du suite jusqu'a ce que l'on obtienne un arbre généalogique (un dendogramme) des ces modalités qui nous indiquera facilement quelles sont celles qui sont proches les unes des autres.
On va appliquer cet algorythme par la méthode de Ward pour distances euclidiennes. Cette façon de faire tend à obtenir chaque regroupement un minimum de distance entre les éléments et/ou un maximum de distance entre les regroupements.
On va appliquer ce calcul sur les coordonnées des lignes et/ou des colonnes d'une AFC, ACM ou ACP.
Reprenons l'AFC faite précédement sur le tablau de l'INSEE :
>afct est l'objet qui contient l'afc sur 6 axes du tableau de contingence vu au point 2.8.2
>afct$row$coord est l'objet qui contient les coodonées des lignes sur 6 axes
>afct$col$coord même chose pour les colonnes
>afct$row$coord->coord_li mettons les dans des objets que l'on créer pour l'occasion
>afct$col$coord->coord_col
On a vu notamment grâce au graphique de l'inertie par axe que les trois premiers axes sont suffisant, recréons donc les objets avec 3 axes au lieu de 6 :
>coord_li[,1:3]->coord_li
>coord_col[,1:3]->coord_col
2.10.1 Arbre pour les modalités colonnes
>dist(coord_col, "euclidian")->dist_col distances euclidiennes entre les modalités>hclust(dist_col, method="ward")->arbre_col créer l'arbre selon la méthode de ward
>plot(arbre_col, main="CAH des modalités colonnes") représente l'arbre

2.10.2 Arbre pour les modalités lignes
On fait la même chose pour les lignes :>dist(coord_li, "euclidian")->dist_li
>hclust(dist_li, method="ward")->arbre_li
>plot(arbre_li, main="CAH des modalités lignes"

2.10.3 Arbre pour les modalités lignes et colonnes
Pour pouvoir éffectuer une CAH des lignes et des colonnes sur le même arbre il va falloir concatener les objets coord_li et coord_col on va utiliser la commande rbind(): >rbind(coord_col,coord_li)->coord
Puis on recommence comme précédemment
>dist(coord, "euclidian")->dist
>hclust(dist, method="ward")->arbre
>plot(arbre, main = "CAH des modalités")

On voit bien sur ce graphique les petits paquets et les proximités entre modalités. On va pouvoir compléter la représentation graphique de notre AFC avec les trois regroupements principaux un peu plus objectivé par la CAH.
3. Références bilbiographiques non-mises en forme
sur R :
Voir la base de donnée bibliographique que j'ai réalisé : http://rndx.tuxfamily.org dans la catégorie "français" ou trouvera des documents dans la langue de Coluche.
Sur les statistiques :
CIBOIS P., Les écarts à l'indépendance, techniques simples pour analyser des données d'enquète sur le site de la revue Sciences Humaines
CIBOIS P., L'analyse des données en sociologie, deuxième édition, Paris : PUF, 1992, coll : le sociologue, 220 pp.
CHAMPAGNE
P., LENOIR R., MERLIE D., PINTO L., Initiation à la pratique
sociologique, DUNOD, Paris : 1999, coll. : psycho sup,
3ème edition, 233 pp.
MAUSS M., Essais de sociologie, Les Editions de Minuit, 1968 et 1969, coll. points essais, 252 pp.
G. MIALARET, Statistiques appliquées aux sciences humaines, Paris : PUF, 1991, 401 pp. coll : fondamental
MONINO J.L., KOSIANSKI J.M., LE CORNU F., Statistiques descriptive, DUNOD, Paris : 2004, coll. : travaux dirigés, 2ème édition, 254 pp.[1]
Un produit scalaire est une opération effectuée entre deux vecteurs qui
permet
d’obtenir une matrice ou un autre vecteur voir notamment G. MIALARET, Statistiques
appliquées aux sciences humaines, Paris : PUF, 1991,
401 p.
coll : fondamental p. 384 ou P. LASCAUX, R. THEODORE, Analyse
numérique
matricielle appliquée à l’art de l’ingénieur : méthodes
directes,
Paris : Dunod, 2000, 317 p., coll : sciences sup p.
21
[2]
G. SAPORTA, Probabilités,
analyse des données et statistiques, Paris :
Technip, 1990, 485 p., p.
207
[3]
P. CIBOIS, L’analyse
factorielle, cinquième édition, Paris : PUF, 2000,
127 p., coll :
Que sais-je ?, p. 121
[4]
C. DERVIN,
Analyse des
correspondances : comment interpréter les
résultats ?, Paris :
STAT-ITCF, 1992, 72 p., p. 41
[5]
L. LEBART,
A. MORINEAU, M. PIRON, Statistique
exploratoire multidimensionnelle, troisième édition,
Paris : Dunod,
2004, 439 p., coll : sciences sup, p. 365-366
[6]
G. SAPORTA, id.,
1990, p. 199
[7]
C. DERVIN, id.,
1992, p. 69
[8]
Y. DODGE, Statistique :
dictionnaire encyclopédique, Paris : Springer, 2004,
624 p., p.38
[9] G. MIALARET, ibid., 1991, p. 384
[10]
P. CIBOIS, id.,
2000, p. 51
[11]
B. ESCOFIER,
J. PAGES, Analyses
factorielles simples et multiples : objectifs, méthodes et
interprétation,
troisième édition, Paris : Dunod, 1998, 284 p. coll :
sciences sup
[12]
J.M. BOUROCHE,
G. SAPORTA, L’analyse
des données, huitième édition, Paris : PUF, 2002,
127 p., coll :
Que sais-je ?
[13]
W. DOISE,
A. CLEMENCE,
F.
LORENZI-CIOLDI, Représentations
sociales et analyses de données, Grenoble : Presse
Universitaire de
Grenoble, 1992, 261 p., p. 107
[14]
B. ESCOFIER,
J. PAGES, id.,
1998, p. 255
[15]
B. ESCOFIER, ibid.,
1998, p. 262
